素數間隙的猜想

尋找素數間隙的通式

兩相鄰素數 (Prime Number) 之間的差，我們叫它為素數間隙 (Prime Gap)，這我們在前一章已介紹過，這一回我們主要討論一些和素數間隙相關的猜想。

瑞典數學家克拉默 (Harald Cramer 1883-1985) 和辛克斯 (Daniel Shanks 1917 - 1996) 也認為這素數間隙長度 (Length of Prime Gap) 為 n 出現的素數 p(n) 是約為：

但波蘭數學家沃爾夫 (Marek Wolf 1956- ) 卻有點不同意見，他認為：

這誰是正確，還有待時日考證。

沃爾夫還對最大素數間隙 (Maximal Prime Gap) 有興趣，即在一定範圍內最大的素數間隙。他認為最大素數間隙 G(n) 約為：

式中 p(n) 為素數個數函數 (Prime Counting Function)，即不少於 n 的素數個數；C₂ 為孿生素數常數 (Twin Primes Constant) ，即

。

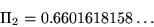我們可把數式簡化為

波歷納克猜想

波歷納克猜想 (Polignac's Conjecture) 當然是由波歷納克 (Alphonse de Polignac 1826-1863) 提出的，是在 1849年：

對每一個偶數 2k (k 不少於 1)，均存在無窮多對相鄰素數 p_n 和 p_n+1 使得 d_n = p_n - p_n+1 = 2k。

特別地，我們若取 k = 1，這便等同攣生素數猜想 (Twin Primes Conjecture)。

別說波歷納克猜想未解決，即使我們把相鄰素數放寬為任意一對素數，問題也是未解決。

安迪加猜想

先讓我們看看一道和素數間隙相關，由羅馬尼亞的數學家安迪加 (Dorin Andrica 1956 - ) 提出的猜想：安迪加猜想 (Andrica's Conjecture)。

安迪加猜想指

其中為第 n 個素數。

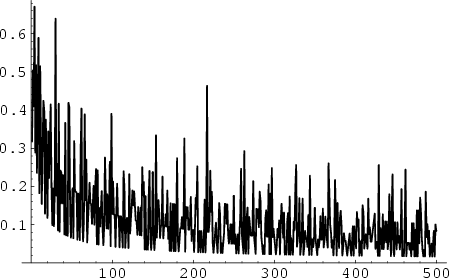
上圖為與 n 的關係，可見在首 500個中最大的一個其實是在開首：

從圖中我們估計是會有一下跌之趨勢，故相關的素數間隙也不可太大。但這只是猜測而已，我們連這是否為 1 所限也未可言證。

我們把安迪加猜想轉移成考慮下式且解出 x：

式中的 P_n 是指第 n 個素數。而 x 的最小值為 x = 0.567148..... 當取素數為 113 及 127 時。而這一 x 值，我們又稱作沙馬雲達基常數 (Smarandache Constant) 。

克拉默猜想

再讓我們看看另一道和素數間隙相關的猜想：克拉默猜想 (Cramer Conjecture)

克拉默認為：

式中的 P_n 是指第 n 個素數。上式的意思為對任何兩相鄰素數而言，其差 (即素數間隙) 與小素數的自然對數 (Natural Logarithm) 值的平方的比不多於 1 。

從下圖可見：

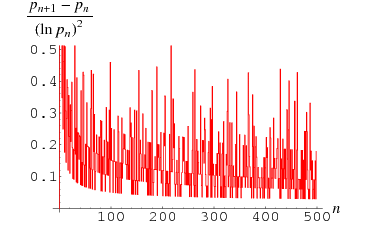
這表可進一步肯定堅信猜想成立是正確的。若猜想成立，可對素數間隙的大小定界，可惜至今尚未有任何證明。

參考文獻及網址：

Ribenboim, P. "The Little Book of Bigger Prime" , New York: Springer-Verlag, 1991

Weisstein, E. W. "Andrica's Conjecture." From MathWorld. http://mathworld.wolfram.com/AndricasConjecture.html.

Weisstein, E. W. "Cramer Conjecture." From MathWorld. http://mathworld.wolfram.com/CramerConjecture.html.

Weisstein, E. W. "Prime Gaps." From MathWorld. http://mathworld.wolfram.com/PrimeGaps.html.

Wolf, M. "First Occurrence of a Given Gap between Consecutive Primes." http://rose.ift.uni.wroc.pl/~mwolf/.

Wolf, M. "Some Conjectures on the Gaps Between Consecutive Primes." http://rose.ift.uni.wroc.pl/~mwolf/.