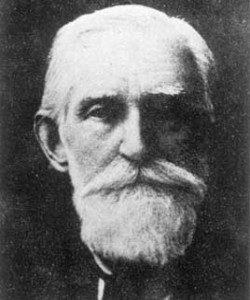素數定理淺介
俄國數學家切比雪夫 (Pafnuty Chebyshev 1821-1894) |
法國數學家阿達瑪 (Jacques Hadamard 1865-1963) |
(照片取自「The MacTutor History of Mathematics Achieve」http://www-gap.dcs.st-and.ac.uk/~history/ )
素數定理 (Prime Number Theorem) 是素數論 (Prime Number Theory) 中最重要的關於素數 個數函數 (Prime Counting Function) p(x) 的理論，讓我為大家介紹這理論的由來和發展。
在素數理論中有許多著名的猜想，都是由經驗中概括過來的，然後再經過嚴格的數學推導，設法加以證明。例如關於 p(x)，即不大於 x 的素數個數，我們稱為素數個數函數。我們因而作了下表：
x |
p(x) |
x / ln(x) |
li (x) |
p(x) / li(x) |
p(x) / x |
1000 |
168 |
145 |
178 |
0.94 |
0.1680 |
10000 |
1229 |
1086 |
1246 |
0.98 |
0.1229 |
50000 |
5133 |
4621 |
5167 |
0.993 |
0.1026 |
100000 |
9592 |
8686 |
9630 |
0.996 |
0.0959 |
500000 |
41538 |
38103 |
41606 |
0.9983 |
0.0830 |
1000000 |
78498 |
72382 |
78628 |
0.9983 |
0.0785 |
2000000 |
148933 |
137848 |
149055 |
0.9991 |
0.0745 |
5000000 |
348513 |
324149 |
348638 |
0.9996 |
0.0697 |
10000000 |
664579 |
620417 |
664918 |
0.9994 |
0.0665 |
20000000 |
1270607 |
1189676 |
1270905 |
0.9997 |
0.0635 |
90000000 |
5216954 |
4913897 |
5217810 |
0.99983 |
0.0580 |
100000000 |
5761455 |
5428613 |
5762209 |
0.99986 |
0.0576 |
1000000000 |
50847478 |
48254630 |
50849235 |
0.99996 |
0.0508 |
我們不難發現 p(x)可能有下列結果：
當 
時，
p(x) 也趨向無限大，這即素數個數有無限多個。詳見另文《天下素數有多少》。
當 時，
p(x) / x 會趨向 0，即幾乎所有自然數是合數。詳見另文《找到素數的概率只有零》。
法國數學家勒讓德 (Adrien-Marie Legendre 1752 - 1833) 在 1830年提出一個猜想：
當 n 很大時，
其中 A=1 及 B = 1.08366。
德國大數學家高斯 (Carl Friedrich Gauss 1777-1855) 又獨立地建議了一個相類似的，但和它不相等的公式，以一千個相繼的自然數為單位，高斯旳方法在於計算每個單位的素數個數，他建議用函數 f(n) = 1 / ln (n) 來表示充分大的整數附近的素數分佈 (Distribution of Primes) 的平均密度 (Mean Density)，因此高斯猜測：
其中 li(x) 為對數積分 (Logarithmic Integral)，即 
。
綜合高斯和勒讓德的工作，我們得：
這便是我們常稱的素數定理。這亦是研究素數分佈的中心定理。因此決定素數定理的正確與否吸引了許多優秀數學工作者的注意，成了許多數學家的目標。
首先對此問題作出貢獻的是俄國數學家切比雪夫 (Pafnuty Chebyshev 1821-1894)，他在 1848年 和 1850年證明了
而最終證明 
= 1。
數學家西爾維斯特 (James Joseph Sylvester 1814-1897) 曾說：但是要確定這種可能性的存在，我們或許要等待世界上產生這樣一個人，他的智慧與洞察力像切比雪夫一樣，證明自己是超人一等的。
就在西爾維斯特說出那番話的時候出生的法國人阿達瑪 (Jacques Hadamard 1865-1963)，依賴前人黎曼 (Georg Friedrich Bernhard Riemann 1826-1866) 的工作，以複分析 (Complex Analysis) 的方法，在 1896年證明了素數定理是正確的。差不多同時而又獨立證明了素數定理的還有比利時人達拉瓦勒布桑 (Charles Jean de la Vallec Poussin 1866-1962) 。
以後尋找一「簡單」的方法，即不以複分析的方法來證明素數定理又成了數學家的新課題。到了 1949 年，才有挪威數學家塞爾伯格 (Atle Selberg 1917- 2007) 和匈牙利數學家愛爾特希 (Paul Erdos 1913-1996) 分別作出獨立證明 ，然而功勞誰大，便促使兩人之間一段長時間的不和。
參考文獻及網址：
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 62-64, 1987.
Weisstein, E. W. "Prime Number Theorem." From MathWorld. http://mathworld.wolfram.com/PrimeNumberTheorem.html.
華羅庚 , 數論導引 , 香港 : 商務印書局 , p. 87 , 1967
