素因子有話兒
素因子的學問
我們知素因子分解 (Prime Factorization) 是一過程把合數 (Composite Number) 分解成一系列素因子 (Prime Factor) 的乘積。現在讓我們來看看這主角 - 素因子有何特別。
最大素因子
最大素因子 (Greatest Prime Factor) 即一數 x 的素因子中最大的一個，簡記 gpf (x)。
如 gpf(10) = 5，gpf(11) = 11等。
若某數 n 的素因子分解式為
則 gpf(n) = max (pi)。
我們可以知道自 2 起最大素因子的數列是這樣的：2, 3, 2, 5, 3, 7, 2, 3, 5, 11, 3, 13, 7, 5, ...... (OEIS A006530)
下圖顯示最大素因子 gpf(n) 與 n 的關係：
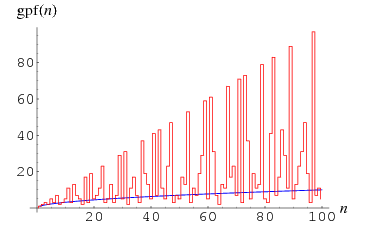
若一數的最大素因子大於其平方根 (Square Root) 的話，我們稱此數為不尋常數 (Unusual Number) 或 粗糙數 (Rough Number) ；反之，一數不是粗糙數，我們稱之為平滑數 (Smooth Number)。
粗糙數有： 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 20, 21, ...... (OEIS A064052)
平滑數有： 1, 4, 8, 9, 12, 16, 18, 24, 25, 27, ...... (OEIS A048098)
不說不知，任意抽一數，抽中粗糙數的概率為 ln 2 ，這是由美國數學家舒賀賓 (Richard C. Schroeppel 1948 - ) 在 1972 年發現的。
最小素因子
最小素因子 (Least Prime Factor) 即一數 x 的素因子中最小的一個，簡記 lpf (x)。
如 lpf(10) = 2，lpf(11) = 11等。
若某數 n 的素因子分解式為
則 lpf(n) = min (pi)。
我們可以知道自 2 起最小素因子的數列是這樣的：2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, ...... (OEIS A020639)
下圖顯示最小素因子 lpf(n) 與 n 的關係：
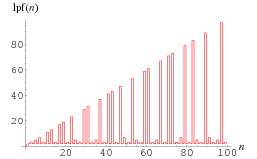
顯然易見，若 n 為一合數，則有 [lpf(n)]2 不少於 n 。
若兩整數 x, y 符合：
x < y
lpf(x) =
lpf(y)
對所有 z, x<z<y
則有 lpf(z) < lpf(x)。
我們稱此 (x,y) 為一孿峰 (Twin Peaks)。從上一關於最小素因子的折線圖中，我們可見一個又一個高隆的「山峰」，而孿峰便是指一對相連等高的「山峰」中找不到其它「山峰」。
我們以 s 表示孿峰兩數之間的距離，即 s = y - x ，但這 s 恆為偶數，故我們可以寫成 s = kp， k 為一偶數。而我們更可把孿峰稱作 kp 孿峰，如一個 4p 孿峰即其間距為 4p。原來孿峰的出現是周期性的，其周期 q = p#，這是 p 的素連乘 (Primorial)，即所有不少於 p 的素數連乘積 (詳可參看《介紹兩個數學符號》)。即若 (x,y) 為一 kp 孿峰，則 (x+q,y+q) 也是一 kp 孿峰。
現在的問題是孿峰是否存在。最先提出這問題的是大衛．威爾遜 (David Wilson) ，是年 1997。接著同日，康韋 (John Horton Conway 1937- ) 、迪莊 (Aise Johan de Jong) 、戴歷．史密夫 (Derek Smith) 及 巴哈迦華 (Manjul Bhargava) 聯合找到了第一組孿峰，p = 113 的 2p 孿峰：(y 可自行以 y = x + 2p 計出來，故不列，下同)
x = 12697 25922 96404 97072 08826 79404 58418 22547 88131
合共有 45 數位之多。這解決了存在性的問題。
接著不久，希倫尼斯 (Fred W. Helenius) 找到了p = 89 和 71 的兩個 2p 孿峰；
p = 89, x = 9503 84492 67493 90990 45485 48436 25839
p = 71, x = 73101 31732 01525 14701 10369
現在已知的最小一對孿峰為 p = 73, x = 20615 19317 17613 27991 10061。欲知更多 2p 孿峰的例子，可參看斯洛恩數列 A009190 。
至於 4p 孿峰的情況又如何，大衛．威爾遜找到了 p = 1327 的一個暫時「最小」的例子和另一個 p = 3203 的例子，但此兩組數值也有相當的大，不便列寫，請見諒。
現在我們與孿峰相關的問題有：
最小孿峰是多少？
4p 孿峰中最小的素數值
p 是多少？
6p 孿峰是否存在？
康威主張孿峰存在上限，這正確嗎？
若 p<q<r
均為素數 (素數的最小素因子是其本身) ，且 p 和 r 均為某 kp 孿峰的成員，是否充要令 q 成為 kp 孿峰的成員呢？
以上問題的答案是開放的，但數學家對此的認識還只是初階而已，還是要由時間把孿峰的經驗積累。
參考文獻及網址：
Weisstein, E. W. "Greatest Prime Factor." From MathWorld. http://mathworld.wolfram.com/GreatestPrimeFactor.html.
Weisstein, E. W. "Least Prime Factor." From MathWorld. http://mathworld.wolfram.com/LeastPrimeFactor.html.
