只有1、2、3 的數列 - 描述數列
美國數學家康韋 (John Horton Conway 1937- )
(照片取自「The MacTutor History of Mathematics Achieve」http://www-gap.dcs.st-and.ac.uk/~history/ )
看看這數列吧
1、11、21、1211、111221、312211、13112221、1113213211、31131211131221、...... (OEIS A005150)
這是一奇怪的數列，只有三個數字 - 1、2 和 3。
這我們稱為描述數列 (Descriptive Sequence) 或 自描數列 (Self-descriptive Sequence) 或 語言數列 (Look And Say Sequence)：總之名字多多。
起始為 1，第二項是描述第一項的結果，即有 1 個 1；第三項是描述第二項的結果，即有 2 個 1；第四項是描述第三項的結果，即有 1 個 2 和 1 個 1：如此下去。
我們不難找到三個結論：
數列是發散的
，而且頗為「快大」。
數列中所有數值的個位恒為 1。
數列中各數值只有三個數字
即 1、2 和 3 所組成。
對於以上第一點，不用多作解釋，文字描述是費時的，哪有數字的簡潔！
第二點，也很自然，數列最後總是描述多少個 1，故新一項數自然是以 1 為個位了。
第三點則用多一丁點時間來解釋吧！若真的出現 4 (或以上的數字)，必然在前一項出現了 4 (或以上的數字) 或是連續出現了 4個 (或更多個) 相同的數字。當然第一個可能性最終推導的源頭也是第二個原因，因為開始為 1 ，不會無故出現 4 或以上的數字。但問題是會不會有 4個 (或更多個) 相同的數字連續出現呢？那就讓我們先看看有 4 個相同數字的情況吧！
假設出現了連續 4 個相同的數字 A，即 ......AAAA...... ，式中 ...... 代表其他數字，下同。若我們自最左 數字開始以數字兩兩一組，那只有兩個可能性，一是這四個 A 分列兩組，即 ...... (AA)(AA) ...... 或置於三組，即 ...... (XA)(AA)(AY)......。
先談第一個可能性，即再前一項出現了 A 個 A 和 A 個 A ，但我們不會把這兩組相同的數字分開描述，只會說一句有 2A 個 A ，故出現這情況是不可能的。而第二個可能性又如何，即再前一項出現了 X 個 A 、A 個 A 和 A 個 Y，我們同樣地把 (X+A) 個 A 分開報數，是不可能的。因此出現 4 或以上的數字是不可能的，除非這個 4 或以上的數字是與生俱來的吧。
至於 0 呢？這更容易解說了，起初不曾有零，故不會說出有若干零這回事；至於有「零個某數」呢，更是說不得。是故我們也不會看到數列中有零了。
若我們開始的不是 1 ，而是其他由 2 至 9 的數字又如何，看看下表：
2 |
2, 12, 1112, 3112, 132112, 1113122112, 311311222112, ...... |
3 |
3, 13, 1113, 3113, 132113, 1113122113, 311311222113, ...... |
4 |
4, 14, 1114, 3114, 132114, 1113122114, 311311222114, ...... |
d |
d, 1d, 111d, 311d, 13211d, 111312211d, 31131122211d, ...... |
上表中 d 為 2 至 9 任何一數。我們不難發現當中的共通。
康韋常數
原來這些描述數列的數值是會漸近一代數式 T(n) = 
，
式中的 
=
1.567......、
=
1.814...... 、
= 1.3035772690342963912570991121525518907307025046594...... ，這
又稱為康韋常數 (Conway's Constant) (OEIS A014715)，而這常數竟是
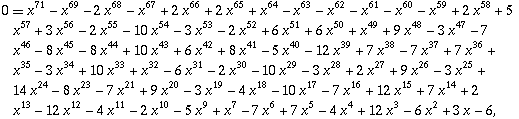
的唯一正實根。
這數列中有素數嗎
如研究以 1 為首的那條描述數列，我們找到當中有 11、 312211、 13112221這三個素數，當然陸續有來的。 那素數我們稱之為描述素數 (Descriptive Prime)。
當中亦有數學家找尋連續的描述素數 (Consecutive Descriptive Primes)，或會否出現描述 素數數鏈 (Chain of Descriptive Primes) 呢？其中康納卡 (G. L. Honaker, Jr.) 便找到 373, 131713, 111311171113, 3113331173113 這一數列，可惜其下一項是一合數。而在 2003年，里弗華 (Carlos B. Rivera, 1950 - )、基思 (Mike Keith 1955 - ) 和 華達．舒尼達 (Walter Schneider) 找到一長七項的描述數列始自 19972667609。會否有更長的描述素數數鏈？我相信會有的。
參考文獻及網址：
Rivera, C. "Problems & Puzzles: Puzzle 036 - Sequences of descriptive primes." http://www.primepuzzles.net/puzzles/puzz_036.htm
Schneider, Walter. "Descriptive Primes" http://www.wschnei.de/digit-related-numbers/descriptive-primes.html
Weisstein, E. W. "Look And Say Sequence." From MathWorld http://mathworld.wolfram.com/LookandSaySequence.html .
談祥柏. "振盪與暴漲的語言數列" 自 樂在其中的數學 , 北京 : 科學出版社 , p. 333-335 , 2005
