把球放進箱子的問題 - 貝爾數
![]()
 美國數學家 貝爾 (Eric Temple Bell 1883-1960) |
 印度數學家拉瑪努江 (Srinivasa Aaiyabgar Ramanujan 1887-1920) |
(照片均取自「The MacTutor History of Mathematics Achieve」http://www-gap.dcs.st-and.ac.uk/~history/ )
![]()
箱子與球的問題
問題:把 3 個有編號的球於進任意多個箱子中 (空箱不作計算),有多少不同的組合 (Combination)?
研究不同組合的問題,我們稱之為組合數學 (Combinatorics),如圖論 (Graph Theory)、幻方 (Magic Square)等也屬這門學科。這是數學中一門更新的分支,當中尚有很多疑團。
返回我們的問題,我們可以一一數算。
我們只用一個箱,把所有球於進一個箱中,有一個組合;
我們只用二個箱,把一球於進其中一個箱中,另外兩個一組放進另一個箱中,這樣有三個組合;
我們用上三個箱,每一個箱放一個球,這樣有一個組合;
合共有五個組合。
那麼四個球又如何呢?
我們只用一個箱,把所有球於進一個箱中,有一個組合;
我們只用二個箱,把一球於進其中一個箱中,另外三個一組放進另一個箱中,這樣有四個組合;
每個箱放兩個球,這樣有 3 個組合;
我們用上三個箱,其中一個放兩個球,另外兩個箱各放一個球,這樣有六個組合;
我們用上四個箱,每一個箱放一個球,這樣有一個組合;
合共有十五個組合。
我們可以看看下圖,圖中的三角形或正方形的每一隻角表示一個球,有直線相連的角,表示那兒的球放進同一個箱中,圖點則表示那個球單獨地放進一個箱子內。
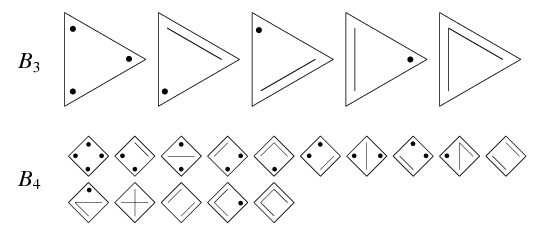
把 n 個有編號的球於進任意多個箱子中的組合數目,我們稱為貝爾數 (Bell Number),記作 Bn, 定義 B0 = B1 = 1。
最初數個貝爾數為 1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, ... (OEIS A000110)
![]()
貝爾數
這是紀念美國數學家及數學史家貝爾 (Eric Temple Bell 1883-1960),他的其中一本著作 "Men of Mathematics: The Lives and Achievements of the Great Mathematicians from Zeno to Poincare" (中譯本為「數學大師:從芝諾到龐加萊, 徐源譯, 上海:上海科技教育出版社, 2004),相信亦有不少朋友看過。貝爾在 1934年發表的論文曾言及此數,但其實最先對此數作詳細研究的為印度數學家拉瑪努江 (Srinivasa Aaiyabgar Ramanujan 1887-1920)。
我們亦可以從另一個角度來看貝爾數。一個含有 n 個不同元素 (Element) 的集合 (Set) S,把它的元素分配於不同的非空子集 (Non - empty Subset) 中,使它們之間的交集 (Intersection) 為空,且所有子集的聯集 (Union) 為 S。貝爾數 Bn 正是那不同分割方法的數目。
我們計算貝爾數可以一個名為貝爾三角形 (Bell Triangle),亦有人稱此為阿特金陣列 (Atiken's Array):
| 1 | |||||
| 1 | 2 | ||||
| 2 | 3 | 5 | |||
| 5 | 7 | 10 | 15 | ||
| 15 | 20 | 27 | 37 | 52 | |
| 52 | 67 | 87 | 114 | 151 | 203 |
首先第一行開始為 1,第二行的第一個數也為 1。
接下自第二行的第二個起,該數等同該行的前一個數和前一行的前一個數的和,如 2 = 1 + 1。
每一行的第一個數為前一行的最尾的一個數,如第三行第一個數便是第二行最尾的那個 2。
如此類推。
讓我們試試為貝爾三角形多添一行吧:
第七行的第一個數源於第六行尾的 203,下一個數為 203 + 52 = 255,下一個數為 255 + 67 = 322,接下來是 322 + 87 = 409 和 409 + 114 = 523,再接下來是 523 + 151 = 674 和 674 + 203 = 877。即 B7 = 877。
| 1 | ||||||
| 1 | 2 | |||||
| 2 | 3 | 5 | ||||
| 5 | 7 | 10 | 15 | |||
| 15 | 20 | 27 | 37 | 52 | ||
| 52 | 67 | 87 | 114 | 151 | 203 | |
| 203 | 255 | 322 | 409 | 523 | 674 | 877 |
此外我們還有一些算式可以計算貝爾數的值的:
![]()
式中的括號為二項式系數 (Binomial Coefficient)。
![]()
另外我們亦有一道與貝爾數相關的同餘式 (Congruence):
![]()
若特取 k = 0,便有下式:
![]()
貝爾數當中的素數 (Prime Number),我們便稱為貝爾素數 (Bell Prime),如 2, 5, 877, 27644437, 35742549198872617291353508656626642567, 359334085968622831041960188598043661065388726959079837 等。(OEIS A051131)
參考文獻及網址:
Weisstein, E. W. "Bell Number." From MathWorld. http://mathworld.wolfram.com/BellNumber.html.
Wikipedia. "Bell Number." From Wikipedia. http://en.wikipedia.org/wiki/Bell_number.
