路徑與素數

迪蘭尼素數

迪蘭尼數 (Delannoy Number) D(a,b) 是指由 (0,0) 至 (a,b)，只可向上、右或右上方向走的可行路徑數。

如 D(2,2) = 16

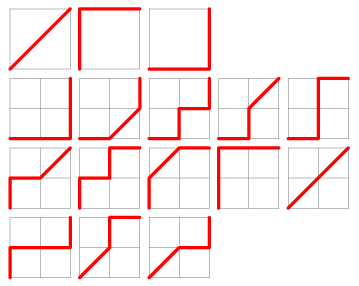
其實我們有一遞推公式 (Recurrence Equation) 求出迪蘭尼數：

D(a,b) = D(a-1,b) + D(a, b-1) + D(a-1,b-1) 其中 D(0,0) = 1

求出迪蘭尼數亦是初中、高小數學競賽中常見的問題。

若取 a = b = n 的話，我們稱作中心迪蘭尼數 (Central Delannoy Number) 的一數列： 3, 13, 63, 321, 1683, 8989, 48639, ...... (OEIS A001850)

其中的素數，即中心迪蘭尼素數 (Central Delannoy Prime) 或迪蘭尼素數 (Delannoy Prime)，首 11000 個迪蘭尼數中就僅有 3, 13, 265729 三個素數 (OEIS A902830) 。

　

莫斯堅素數

莫斯堅數 (Motzkin Number) 的定義和迪蘭尼數相若，不過這次是考慮由 (0,0) 至 (n,0) 的可行路徑數，但只可向右上、右下或正右方向走，這簡記為 M(n) 或 M_n。

如 M₀ = 1, M₁ = 1, M₂ = 2, ....

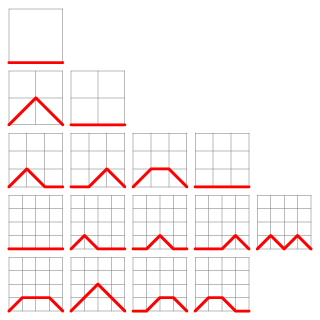
我們可以用一遞推公式求出莫斯堅數：

M_n = (n+2)^-1 * [3(n-1)M_n-2 + (2n+1)M_n-1]

其中 M₀ = 1, M₁ = 1。

其中的素數，即莫斯堅素數 (Motzkin Prime) ，首 263000 個莫斯堅數中就僅有 2, 127, 15511, 953467954114363 四個素數 (OEIS A902832) 。

　

參考文獻及網址：

Weisstein, E. W. "Delannoy Number." From MathWorld. http://mathworld.wolfram.com/DelannoyNumber.html.

Weisstein, E. W. "Motzkin Number." From MathWorld. http://mathworld.wolfram.com/MotzkinNumber.html.