歐拉常數與素數

瑞士數學家歐拉 (Leonhard Euler 1707-1783)

(照片取自「The MacTutor History of Mathematics Achieve」http://www-gap.dcs.st-and.ac.uk/~history/ )

　

歐拉無處不在

瑞士數學家歐拉 (Leonhard Euler 1707-1783) 對數學所作的貢獻多的事，縱然他年輕時已右眼失明，未及六十歲連僅餘一隻眼的視力也因為白內障而失掉，這無阻他對數學的貢獻，他的影響到處可見。

歐拉常數 (Euler's Constant)，又稱為歐拉 - 馬歇羅尼常數 (Euler-Mascheroni Constant)，簡稱歐拉常數。此常數最先由歐拉於 1781 年提出，並求至 16 小數位。1790 年，意大利數學家馬歇羅尼 (Lorenzo Mascheroni 1750-1800) 得至 32 位小數，並使用現在常用的簡記 g，希臘字母，音 Gamma。可惜他的計算當中僅首 19 小數位準確。該常數因而以歐拉 - 馬歇羅尼常數為名。

　

歐拉常數的定義為：

g =

若以定積分 (Definite Integral) 表示，則是：

g = = =

若以二重積分 (Double Integral) 表示，則是：

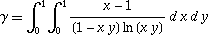
我們亦可以麥爾滕定理 (Mertens Theorem)，計算歐拉常數的值：

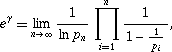
式中 p 為素數，若在式子兩邊取對數，則得：

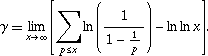
歐拉常數亦可以數列表示：

那麼，歐拉常數值多少？那是 g = 0.577215664901532860606512090082402431042...... (OEIS A001620)

　

素數此中尋

和別的常數一樣，我們定義歐拉常數數列 (Euler Constant Sequence) 或 g 數列 ( g - Sequence)：

5, 57, 577, 5772, 57721, 577215, 5772156, 57721566, 577215664, 5772156649, 57721566490, 577215664901, ......

　

當中的素數，便是歐拉常數素數 (Euler Constant Prime) 或 g 素數 ( g - Prime)。

歐拉常數素數計有 5, 577, 5772156649015328606065120900824024310421 等 (OEIS A072952)。它們的數位分別是 1, 3, 40, 185, 1038, 22610 等 (OEIS A065815)。

　

參考文獻及網址：

Weisstein, E. W. "Constant Primes." From MathWorld. http://mathworld.wolfram.com/ConstantPrimes.html.

Weisstein, E. W. "Euler-Mascheroni Constant." From MathWorld. http://mathworld.wolfram.com/Euler-MascheroniConstant.html.

Bell, E. T. "Men of Mathematics: The Lives and Achievements of the Great Mathematicians from Zeno to Poincare", 1937