黃金比與素數

「黃金比」中沒有黃金

黃金比 (Golden Ratio) 和黃金沒有任何關係，看此文者別奢想得到黃金。

黃金比又稱黃金分割 (Golden Section)、完美比例 (Divine Proportion)、黃金中值 (Golden Mean) 等，可見古希臘人對此數的尊崇。此值簡記為 f，希臘字母，音 phi。

黃金比定義如下：

　

在幾何的意義是把一個長闊為 f 及 1 的長方形分成兩部分，一個 1 x 1 的正方形及餘下的新長方形。選取合宜的數值 f 使新舊長方形相似。

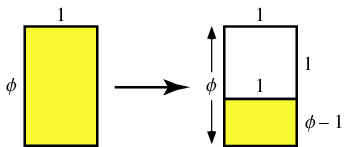
換成代數方程，便得 ，解得 f = 。

即 f = 1.618033988749894848204586834365 ...... (OEIS A001622)

　

我們又可以下式表示黃金比：

即把一長 1+ f 的線段分成兩部分，即 1 和 f ，使 f 和全長的比等於兩部分的比。

我們亦可以一美麗的根式表示黃金比：

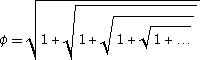
我們亦知道黃金比和費波拿契數 (Fibonacci Number) 有樣十分密切的關係，因為兩相鄰費波拿契數的比的極限正正就是黃金比。

古希臘人稱此數為黃金比，是因為這數太完美了，像黃金一樣。事實上很多我們看來美的構圖中，也找得著黃金比。

　

「黃金比」中也有素數

和其他常數 (Constant) 一樣，我們又定義一常數數列 (Constant Sequence)，名為黃金比數列 (Golden Ratio Sequence) 或 f 數列 ( f - Sequence 或 Phi - Sequence)。

即 1, 16, 161, 1618, 16180, 161803, 1618033, 16180339, 161803398, 1618033988, 16180339887, 161803398874, ......

　

當中找到素數嗎？若有，便是黃金比素數 (Golden Ratio Prime)，簡記 f 素數 ( f - Prime 或 Phi - Prime)。

答案是有的：

包括 1618033、1618033988749、...... (OEIS A064117)，它們分別是有含有 7, 13, 255, 280, ...... (OEIS A064119) 個數位之多。但在 48885 數位以內，也未見第五個黃金比素數：黃金是罕有一些的。

　

參考文獻及網址：

Weisstein, E. W. "Constant Primes." From MathWorld. http://mathworld.wolfram.com/ConstantPrimes.html.

Weisstein, E. W. "Golden Ratio." From MathWorld. http://mathworld.wolfram.com/GoldenRatio.html.

Weisstein, E. W. "Phi-Prime." From MathWorld. http://mathworld.wolfram.com/Phi-Prime.html.