談談素數圓
![]()
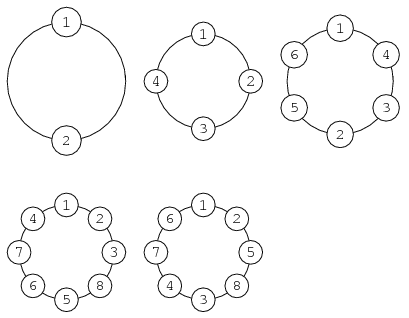
所謂素數圓 (Prime Circle),便是把 1 至 2n 的整數排成一圓 (即首尾相接),使當中任何兩個左鄰右里的數字相加也是素數。
如:
這問題是環排列 (Circular Permutation) 問題的一個特例。其實排列 (Permutation) 是組合數學 (Combinatorics) 中一類基本的課題,研究在 n 個元素中任意取 r 個元素的不同方法,記作 Prn 。
Prn = n! / (n-r)! = n * (n-1) * ...... * (n-r+1)
而所謂環排列問題,即把自 1 至 n 的整數排成一圓,看看有多少不同的排列方法,由於在一圓中是首尾相接,故環排列的數值是比排列為少。試想像把 n 個人置於圓桌上的 r 個不同位置,其環排列數目記作 Qrn 。而 我們知道序列 (1, 2, 3, ..... , r) 和 (r, 1, 2, ...... , r-1) 和 (r-1, r, 1, ..... , r-2) 等在環排列上被視作一樣,故我們有 r 個結果相同,因而有
Qrn = Prn / r
特別是
Qmm = Pmm / m = m! / m = (m-1)!
而現在我們只考慮當 m 為偶數 ,即 m = 2n ,及當中的一些特殊情況。其實當用 2、4或 6 個整數來作素數環也只有一個排列方法,而用 8 個數字則有兩個不同的排列方法 (如上圖)。到底對每一個 n 而言,有多少個不同的排列方法呢?
答案是:1, 1, 1, 2, 48, 512, ...... (OEIS A051252)
參考文獻及網址:
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 105-106, 1994.
Weisstein, E. W. "Prime Circle." From MathWorld. http://mathworld.wolfram.com/PrimeCircle.html.
