再談丟勒幻方

一切由憂鬱開始

在西方，德國藝術家丟勒 (Albrecht Durer 1471-1528) 在 1514 年繪製的名畫《憂鬱》 (Melencolia I)，這可能是最具數學意識的藝術品之一。這板畫當中也包含了一個四階幻方，我們可稱這類幻方為丟勒幻方 (Durer's Magic Square)。

在圖的右上方，我們可見這個四階的丟勒幻方。

16	3	2	13
5	10	11	8
9	6	7	12
4	15	14	1

這個幻方被譽為完美幻方，正因為當中很多組合的和也等同幻和 (Magic Sum) ，即 34。本人在另文《由洛書到名畫 - 幻方欣賞一》已講解過這個幻方的一些性質，這兒不作冗列了。但不可不提，我們可以用製作這個幻方的方法來製作三樣東西：一是鏡反幻方 (Mirror Magic Square)、二是更高階的丟勒幻方 (Durer's Magic Square)、三是由更高階的丟勒幻方而變化出來的更高階鏡反幻方。

丟勒幻方的秘密

其實製作丟勒幻方亦不難。我們可先把一個四四一十六的方陣的對角線著色：

然後我們在第一行，由右至左填上 1 至 4 ，在第二和第三行則沿左至右分別填上 5 至 8 和 9 至 12，而最末一行則和第一行相同，沿右至左填上 13 至 16。

簡單而言，第一行由右至左 (當然由左至右亦可以)，接下來偶數行的填向和上一行相反，而奇數行的填向則和上一行相同。便得下圖。

4	3	2	1
5	6	7	8
9	10	11	12
16	15	14	13

把灰格的數字作上下反射：

16	3	2	13
5	10	11	8
9	6	7	12
4	15	14	1

這個製造幻方的方法，我們稱為丟勒法 (Durer's Method)。

熟悉製作幻方的網友或會留意到，丟勒法和通常製作偶階幻方 (Even Ordered Magic Square) 的對角線法 (Diagonal Method) 有點像樣。的確如此，但也有不同的地方：

丟勒法只適用於 4 或以上的 2 的方冪，而對角線法適用 4 或以上的所有偶數。

丟勒法每橫行的數字序向都不一樣，但對角線法中的是相同。

丟勒法是把對角線上的數字作上下鏡反，但對角線法是作一百八十度旋轉。

作高階丟勒幻方時得作第二次的左右鏡反，其實在原四階丟勒幻方亦可作相類似的左右鏡反，但事實上沒有而已。而對角線法只是一次過作位置變換，而非分兩次對不同的對象作位置變換。

總結兩者不同之處亦很多，該不易運亂的。

八階和十六階的丟勒幻方

我們可把類此的方法擴展至八階或任何階數為二的方冪的幻方之中。現在讓我們看看八階幻方的例子：

首先我們把當中每個四階的小幻方的對角線著色。再依下列方向：第一、四、五、八行由右至左；其餘四行由左至右填上 1 至 64。

8	7	6	5	4	3	2	1
9	10	11	12	13	14	15	16
17	18	19	20	21	22	23	24
32	31	30	29	28	27	26	25
40	39	38	37	36	35	34	33
41	42	43	44	45	46	47	48
49	50	51	52	53	54	55	56
64	63	62	61	60	59	58	57

再把灰格的數字作上下鏡反：

64	7	6	61	60	3	2	57
9	50	51	12	13	54	55	16
17	42	43	20	21	46	47	24
40	31	30	37	36	27	26	33
32	39	38	29	28	35	34	25
41	18	19	44	45	22	23	48
49	10	11	52	53	14	15	56
8	63	62	5	4	59	58	1

我們發現這幻方也是一個關聯幻方，且其橫看第一、二行兩格中的數字之和，第三、四行兩格中的數字之和，第五、六行兩格及最末兩行兩格中的數字之和形成如下左表的規律。反過來，我們直行每兩格的數字之和也形成右圖的規律：

71	67	63	59
59	63	67	71
59	63	67	71
71	67	63	59
71	67	63	59
59	63	67	71
59	63	67	71
71	67	63	59

73	57	57	73	73	57	57	73
57	73	73	57	57	73	73	57
73	57	57	73	73	57	57	73
57	73	73	57	57	73	73	57

這已是一個幻方了。但問題來了，這似乎和原有的丟勒幻方有點不相同：原來的四階幻方中兩相鄰元素之和，不論直行還是橫行，也只有兩種不同的數值；但現在的左圖卻混進了四個不同的數值。

解決方法是得再作一次橫向的變換，而這個變換是原來四階的丟勒幻方中沒有的：

64	7	6	61	60	3	2	57
9	50	51	12	13	54	55	16
17	42	43	20	21	46	47	24
40	31	30	37	36	27	26	33
32	39	38	29	28	35	34	25
41	18	19	44	45	22	23	48
49	10	11	52	53	14	15	56
8	63	62	5	4	59	58	1

對，又是看著灰色的格，但這回是左右鏡反：

64	2	3	61	60	6	7	57
9	55	54	12	13	51	50	16
17	47	46	20	21	43	42	24
40	26	27	37	36	30	31	33
32	34	35	29	28	38	39	25
41	23	22	44	45	19	18	48
49	15	14	52	53	11	10	56
8	58	59	5	4	62	63	1

即成下圖的製成品：

64	2	3	61	60	6	7	57
9	55	54	12	13	51	50	16
17	47	46	20	21	43	42	24
40	26	27	37	36	30	31	33
32	34	35	29	28	38	39	25
41	23	22	44	45	19	18	48
49	15	14	52	53	11	10	56
8	58	59	5	4	62	63	1

這個新的幻方，橫看相鄰兩行的和分別是 64 和 66，而直看鄰兩行的和分別是 73 和 57：

66	64	66	64
64	66	64	66
64	66	64	66
66	64	66	64
66	64	66	64
64	66	64	66
64	66	64	66
66	64	66	64

73	57	57	73	73	57	57	73
57	73	73	57	57	73	73	57
73	57	57	73	73	57	57	73
57	73	73	57	57	73	73	57

這樣，只要我們選擇和分別為 64 及 66 的數組各兩對，或和分別為 57 及 73 的數組各兩對，便可湊足 260 這個幻和了。當然該幻方亦是一個關聯幻方 (Associative Magic Square)，即找依中央作旋轉對稱的兩點的和會是 65，這樣任找四對，亦可湊足 260來。

丟勒或然沒有以此法創製八階幻方，但這其實不是一個新創的幻方，因為和丟勒差不多相同時期的另一人，德國哲學家、神學家兼天文學家阿格里帕 (Heinrich Cornelius Agrippa 1486-1535) 早對幻方有研究。大約 1510年，他製作了三階至九階的幻方，分別冠以土星 (Saturn) 、木星 (Jupiter) 、火星 (Mars) 、太陽 (Sol) 、金星 (Venus) 、水星 (Mercury) 和月亮 (Luna) 的名字，其中四階和八階幻方正和我們討論的幻方結構相同。

說回那個八階幻方，各行元素的平方和也是成雙成對的出現：不論橫直，第四、五行的平方和是相同的，第三、六行的平方和也是相同；第二、七行和第一、八行亦然：不信的話，拿計算機出來計一計便知曉。順便一言，直行，第四、三、二、一行的平方和分別為 11140、11156、11188 和 11236 ，這四數成一道二次算術數列 (Arithmetic Sequence)，即兩相鄰數字的差成一公差為 16 的算術數列；而橫行，第四、三、二、一行的平方和分別為 8620、9644、11692 和 14764，這四數亦成一道二次算術數列，而兩相鄰數字的差這回成一公差為 1024 的算術數列。若階數為 n = 8，則此兩公差，一為 2n，一為 2n³。這現象在原有的四階丟勒幻方中看不見，但在接下來的十六階丟勒幻方中則可印證。

以下來是十六階的丟勒幻方：

256	2	3	253	252	6	7	249	248	10	11	245	244	14	15	241
17	239	238	20	21	235	234	24	25	231	230	28	29	227	226	32
33	223	222	36	37	219	218	40	41	215	214	544	45	211	210	48
208	50	51	205	204	54	55	201	200	58	59	197	196	62	63	193
192	66	67	189	188	70	71	185	184	74	75	181	180	78	79	177
81	175	174	84	85	171	170	88	89	167	166	92	93	163	162	96
97	159	158	100	101	155	154	104	105	151	150	108	109	147	146	112
144	114	115	141	140	118	119	137	136	122	123	133	132	126	127	129
128	130	131	125	124	134	135	121	120	138	139	117	116	142	143	113
145	111	110	148	149	107	106	152	143	103	102	156	127	99	98	160
161	95	94	164	165	91	90	168	169	87	86	172	173	83	82	176
80	178	179	77	76	182	183	73	72	186	187	69	68	190	191	65
64	194	195	61	60	198	199	57	56	202	203	53	52	206	207	49
209	47	46	212	213	43	42	216	217	39	38	220	221	35	34	224
225	31	30	228	229	27	26	232	233	23	22	236	237	19	18	240
16	242	243	13	12	246	247	9	8	250	251	5	4	254	255	1

這個幻方，橫看相鄰兩行的和分別是 256 和 258，而直看鄰兩行的和分別是 241 和 273。看看要找出幻和 2056 的組合也不難呢。

此外，這幻方中各行的平方和也是左右或上下對稱的，如第一行和第十六行的平方和是相同的，或第八行和第九行的平方和也相同等。直行，第八至第一行的平方和分別為 351240、351272、351336、351432、351560、351720、351912 和 352136，這是一道公差為 32 的二次算術數列；而橫看，第八至第一行的平方和分別為 8192、16384、24576、32768、40960、49152 和 57344，這便是一道公差為 8192 的二次算術數列。我們亦看到 32 = 2*16 ，8192 = 2*16*16*16，這不印證我們剛才在八階丟勒幻方看到的事情嗎？

再高一階又如何？那便是三十二階了，合共有 1024 個格得填上，以這方法製不算太難，只是得花點時間而已。

拿片鏡子照幻方

所謂鏡反幻方，即把整個幻方作上下或左右鏡反 (Reflection)，鏡像依然是一個幻方。由於得把幻方連同數字作鏡反，故我們只可使用 1、8 或 0 或其組成的數字填進幻方中。當然若然我們不是要鏡反，而是要求旋轉 (Rotation) 的話，2、5、6、9也可使用的。

若我們四階的丟勒幻方中各值減一，再轉為二進制，便得到一個鏡反幻方來：

1111	0010	0001	1100
0100	1001	1010	0111
1000	0101	0110	1011
0011	1110	1101	0000

但是以零作為一數之始，總感不妙，故得把幻方數字中的 0 更換成 8。廣東人「八」喻意「發財」，所以我說這是一個「意頭」極佳的幻方：

1111	8818	8881	1188
8188	1881	1818	8111
1888	8181	8118	1811
8811	1118	1181	8888

其實我們把 0 和 1 代換成任何不同的數字，結果也成幻方。

幻方中每一個數字也是上下對稱，也和自身或別數字成左右對稱，而其幻和是 19998，同時亦符合原幻方的各項條件，怪不怪哉？其實這因由很簡單，因直、橫或對角線各行中的四個數字合共使每個數位均有兩個 0 和兩個 1。而不論把零和一代換成任何不同的數字，即數字出現的次數也相同，其和自然也相同了。

誠如先前所述，若把這鏡反幻方左右或上下反射，也成另一個幻方。現在我們反一反，看一看吧：

8811	1888	8188	1111
1118	8181	1881	8818
1181	8118	1818	8881
8888	1811	8111	1188

8811	1118	1181	8888
1888	8181	8118	1811
8188	1881	1818	8111
1111	8818	8881	1188

其實我們把這個幻方作一百八十度旋轉，又會得出一個「意頭」極佳的幻方來：

8888	1811	8111	1188
1181	8118	1818	8881
1118	8181	1881	8818
8811	1888	8188	1111

外國人亦以 IXOHOXI 來稱呼此類幻方，單看名字已知這幻方的反射對稱特性了。

再看八階的鏡反幻方：

111111	888881	888818	111188	111811	888181	888118	111888
881888	118118	118181	881811	881188	118818	118881	881111
818888	181118	181181	818811	818188	181818	181881	818111
188111	811881	811818	188188	188811	811181	811118	188888
811111	188881	188818	811188	811811	188181	188118	811888
181888	818118	818181	181811	181188	818818	818881	181111
118888	881118	881181	118811	118188	881818	881881	118111
888111	111881	111818	888188	888811	111181	111118	888888

看到個幻方，我不禁想起《易經》和《六十四卦》來。

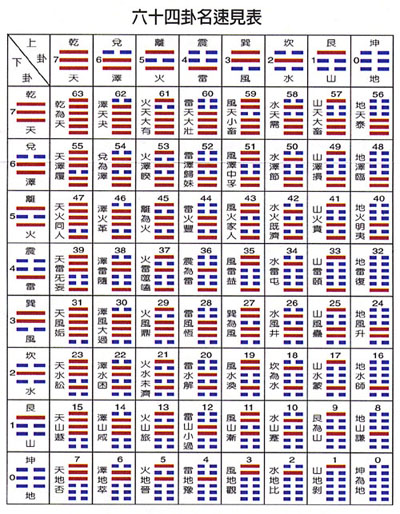
其實我們看《易經》也不用看得太過神化，那不過以陰陽組合代表八樣自然的東西 (八卦)，再由此衍生出六十四樣與自然、生活等有關的事情來，訴出一些處世的哲學而已。而陰陽我們可以以一和零表示，故六十四卦便等同一組六位的二進制數了。我現在不過把這六十四個數排在一個幻方中而已。

再來一個十六階的鏡反幻方：

11118888	88881118	88881181	11118811	11118188	88881818	88881881	11118111	11111888	88888118	88888181	11111811	11111188	88888818	88888881	11111111
88811111	11188881	11188818	88811188	88811811	11188181	11188118	88811888	88818111	11181881	11181818	88818188	88818811	11181181	11181118	88818888
88181111	11818881	11818818	88181188	88181811	11818181	11818118	88181888	88188111	11811881	11811818	88188188	88188811	11811181	11811118	88188888
11888888	88111118	88111181	11888811	11888188	88111818	88111881	11888111	11881888	88118118	88118181	11881811	11881188	88118818	88118881	11881111
18118888	81881118	81881181	18118811	18118188	81881818	81881881	18118111	18111888	81888118	81888181	18111811	18111188	81888818	81888881	18111111
81811111	18188881	18188818	81811188	81811811	18188181	18188118	81811888	81818111	18181881	18181818	81818188	81818811	18181181	18181118	81818888
81181111	18818881	18818818	81181188	81181811	18818181	18818118	81181888	81188111	18811881	18811818	81188188	81188811	18811181	18811118	81188888
18888888	81111118	81111181	18888811	18888188	81111818	81111881	18888111	18881888	81118118	81118181	18881811	18881188	81118818	81118881	18881111
81118888	18881118	18881181	81118811	81118188	18881818	18881881	81118111	81111888	18888118	18888181	81111811	81111188	18888818	18888881	81111111
18811111	81188881	81188818	18811188	18811811	81188181	81188118	18811888	18818111	81181881	81181818	18818188	18818811	81181181	81181118	18818888
18181111	81818881	81818818	18181188	18181811	81818181	81818118	18181888	18188111	81811881	81811818	18188188	18188811	81811181	81811118	18188888
81888888	18111118	18111181	81888811	81888188	18111818	18111881	81888111	81881888	18118118	18118181	81881811	81881188	18118818	18118881	81881111
88118888	11881118	11881181	88118811	88118188	11881818	11881881	88118111	88111888	11888118	11888181	88111811	88111188	11888818	11888881	88111111
11811111	88188881	88188818	11811188	11811811	88188181	88188118	11811888	11818111	88181881	88181818	11818188	11818811	88181181	88181118	11818888
11181111	88818881	88818818	11181188	11181811	88818181	88818118	11181888	11188111	88811881	88811818	11188188	11188811	88811181	88811118	11188888
88888888	11111118	11111181	88888811	88888188	11111818	11111881	88888111	88881888	11118118	11118181	88881811	88881188	11118818	11118881	88881111

相信大家看到這麼多 8 和 1 ，定必頭暈了。

但我還是欣賞鏡反幻方的對稱美和意頭好，是故特意精選字體，把四階和八階的鏡反幻方製成文本 IXOHOXI.pdf，以供諸君下載。新年拿張來當作揮春亦可以，上下左右怎貼也可。

參考文獻及網址：

Heinz, H. "More Magic Square." From Magic Hypercube Hompage http://www.magic-squares.net/moremsqrs.htm.

Pickover, C. A. The Zen of Magic Squares, Circles, and Stars. New Jersey : Princeton University Press , 2002

8	7	6	5	4	3	2	1
9	10	11	12	13	14	15	16
17	18	19	20	21	22	23	24
32	31	30	29	28	27	26	25
40	39	38	37	36	35	34	33
41	42	43	44	45	46	47	48
49	50	51	52	53	54	55	56
64	63	62	61	60	59	58	57

64	7	6	61	60	3	2	57
9	50	51	12	13	54	55	16
17	42	43	20	21	46	47	24
40	31	30	37	36	27	26	33
32	39	38	29	28	35	34	25
41	18	19	44	45	22	23	48
49	10	11	52	53	14	15	56
8	63	62	5	4	59	58	1

64	7	6	61	60	3	2	57
9	50	51	12	13	54	55	16
17	42	43	20	21	46	47	24
40	31	30	37	36	27	26	33
32	39	38	29	28	35	34	25
41	18	19	44	45	22	23	48
49	10	11	52	53	14	15	56
8	63	62	5	4	59	58	1

64	2	3	61	60	6	7	57
9	55	54	12	13	51	50	16
17	47	46	20	21	43	42	24
40	26	27	37	36	30	31	33
32	34	35	29	28	38	39	25
41	23	22	44	45	19	18	48
49	15	14	52	53	11	10	56
8	58	59	5	4	62	63	1

64	2	3	61	60	6	7	57
9	55	54	12	13	51	50	16
17	47	46	20	21	43	42	24
40	26	27	37	36	30	31	33
32	34	35	29	28	38	39	25
41	23	22	44	45	19	18	48
49	15	14	52	53	11	10	56
8	58	59	5	4	62	63	1

256	2	3	253	252	6	7	249	248	10	11	245	244	14	15	241
17	239	238	20	21	235	234	24	25	231	230	28	29	227	226	32
33	223	222	36	37	219	218	40	41	215	214	544	45	211	210	48
208	50	51	205	204	54	55	201	200	58	59	197	196	62	63	193
192	66	67	189	188	70	71	185	184	74	75	181	180	78	79	177
81	175	174	84	85	171	170	88	89	167	166	92	93	163	162	96
97	159	158	100	101	155	154	104	105	151	150	108	109	147	146	112
144	114	115	141	140	118	119	137	136	122	123	133	132	126	127	129
128	130	131	125	124	134	135	121	120	138	139	117	116	142	143	113
145	111	110	148	149	107	106	152	143	103	102	156	127	99	98	160
161	95	94	164	165	91	90	168	169	87	86	172	173	83	82	176
80	178	179	77	76	182	183	73	72	186	187	69	68	190	191	65
64	194	195	61	60	198	199	57	56	202	203	53	52	206	207	49
209	47	46	212	213	43	42	216	217	39	38	220	221	35	34	224
225	31	30	228	229	27	26	232	233	23	22	236	237	19	18	240
16	242	243	13	12	246	247	9	8	250	251	5	4	254	255	1

8	7	6	5	4	3	2	1
9	10	11	12	13	14	15	16
17	18	19	20	21	22	23	24
32	31	30	29	28	27	26	25
40	39	38	37	36	35	34	33
41	42	43	44	45	46	47	48
49	50	51	52	53	54	55	56
64	63	62	61	60	59	58	57

64	7	6	61	60	3	2	57
9	50	51	12	13	54	55	16
17	42	43	20	21	46	47	24
40	31	30	37	36	27	26	33
32	39	38	29	28	35	34	25
41	18	19	44	45	22	23	48
49	10	11	52	53	14	15	56
8	63	62	5	4	59	58	1

64	7	6	61	60	3	2	57
9	50	51	12	13	54	55	16
17	42	43	20	21	46	47	24
40	31	30	37	36	27	26	33
32	39	38	29	28	35	34	25
41	18	19	44	45	22	23	48
49	10	11	52	53	14	15	56
8	63	62	5	4	59	58	1

64	2	3	61	60	6	7	57
9	55	54	12	13	51	50	16
17	47	46	20	21	43	42	24
40	26	27	37	36	30	31	33
32	34	35	29	28	38	39	25
41	23	22	44	45	19	18	48
49	15	14	52	53	11	10	56
8	58	59	5	4	62	63	1

64	2	3	61	60	6	7	57
9	55	54	12	13	51	50	16
17	47	46	20	21	43	42	24
40	26	27	37	36	30	31	33
32	34	35	29	28	38	39	25
41	23	22	44	45	19	18	48
49	15	14	52	53	11	10	56
8	58	59	5	4	62	63	1

256	2	3	253	252	6	7	249	248	10	11	245	244	14	15	241
17	239	238	20	21	235	234	24	25	231	230	28	29	227	226	32
33	223	222	36	37	219	218	40	41	215	214	544	45	211	210	48
208	50	51	205	204	54	55	201	200	58	59	197	196	62	63	193
192	66	67	189	188	70	71	185	184	74	75	181	180	78	79	177
81	175	174	84	85	171	170	88	89	167	166	92	93	163	162	96
97	159	158	100	101	155	154	104	105	151	150	108	109	147	146	112
144	114	115	141	140	118	119	137	136	122	123	133	132	126	127	129
128	130	131	125	124	134	135	121	120	138	139	117	116	142	143	113
145	111	110	148	149	107	106	152	143	103	102	156	127	99	98	160
161	95	94	164	165	91	90	168	169	87	86	172	173	83	82	176
80	178	179	77	76	182	183	73	72	186	187	69	68	190	191	65
64	194	195	61	60	198	199	57	56	202	203	53	52	206	207	49
209	47	46	212	213	43	42	216	217	39	38	220	221	35	34	224
225	31	30	228	229	27	26	232	233	23	22	236	237	19	18	240
16	242	243	13	12	246	247	9	8	250	251	5	4	254	255	1

8	7	6	5	4	3	2	1
9	10	11	12	13	14	15	16
17	18	19	20	21	22	23	24
32	31	30	29	28	27	26	25
40	39	38	37	36	35	34	33
41	42	43	44	45	46	47	48
49	50	51	52	53	54	55	56
64	63	62	61	60	59	58	57

64	7	6	61	60	3	2	57
9	50	51	12	13	54	55	16
17	42	43	20	21	46	47	24
40	31	30	37	36	27	26	33
32	39	38	29	28	35	34	25
41	18	19	44	45	22	23	48
49	10	11	52	53	14	15	56
8	63	62	5	4	59	58	1

64	7	6	61	60	3	2	57
9	50	51	12	13	54	55	16
17	42	43	20	21	46	47	24
40	31	30	37	36	27	26	33
32	39	38	29	28	35	34	25
41	18	19	44	45	22	23	48
49	10	11	52	53	14	15	56
8	63	62	5	4	59	58	1

64	2	3	61	60	6	7	57
9	55	54	12	13	51	50	16
17	47	46	20	21	43	42	24
40	26	27	37	36	30	31	33
32	34	35	29	28	38	39	25
41	23	22	44	45	19	18	48
49	15	14	52	53	11	10	56
8	58	59	5	4	62	63	1

64	2	3	61	60	6	7	57
9	55	54	12	13	51	50	16
17	47	46	20	21	43	42	24
40	26	27	37	36	30	31	33
32	34	35	29	28	38	39	25
41	23	22	44	45	19	18	48
49	15	14	52	53	11	10	56
8	58	59	5	4	62	63	1

256	2	3	253	252	6	7	249	248	10	11	245	244	14	15	241
17	239	238	20	21	235	234	24	25	231	230	28	29	227	226	32
33	223	222	36	37	219	218	40	41	215	214	544	45	211	210	48
208	50	51	205	204	54	55	201	200	58	59	197	196	62	63	193
192	66	67	189	188	70	71	185	184	74	75	181	180	78	79	177
81	175	174	84	85	171	170	88	89	167	166	92	93	163	162	96
97	159	158	100	101	155	154	104	105	151	150	108	109	147	146	112
144	114	115	141	140	118	119	137	136	122	123	133	132	126	127	129
128	130	131	125	124	134	135	121	120	138	139	117	116	142	143	113
145	111	110	148	149	107	106	152	143	103	102	156	127	99	98	160
161	95	94	164	165	91	90	168	169	87	86	172	173	83	82	176
80	178	179	77	76	182	183	73	72	186	187	69	68	190	191	65
64	194	195	61	60	198	199	57	56	202	203	53	52	206	207	49
209	47	46	212	213	43	42	216	217	39	38	220	221	35	34	224
225	31	30	228	229	27	26	232	233	23	22	236	237	19	18	240
16	242	243	13	12	246	247	9	8	250	251	5	4	254	255	1