連續素幻方

所謂幻方 (Magic Square) 又稱魔方、魔方陣等，即把一系列不同的整數排放在一 n*n 的方陣內使得每一直行、橫行或對角線 (Diagonal) 的 n 個數字總和相等。

而連續素幻方 (Consecutive Prime Magic Square) ，則是把連續素數 (Consecutive Primes) 填在方陣中使成為幻方。若人給予尋找三階連續素幻方的人獎金的話，大家不妨猜一猜一個三階連續素幻方值多少獎金。

答案是一百美元，屬多屬少，看看那幻方先吧！

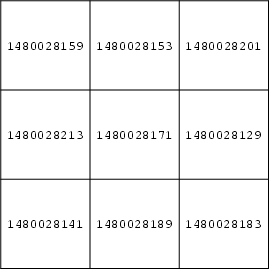
故事是這樣的：在 1988年，美國人數學普及大師馬丁．加納德 (Martin Gardner 1914 - 2010) 在意大利羅馬設計並出版了張掛牆的年曆，年曆的主角不是名車、風景或美女，而是一幅關於「素數幻方」的畫，名為「1988年數學掛曆」。大家或會想這掛曆誰人會購買，我真不知到！

　

所謂素數幻方是指一個三階 (縱橫各 3 格) 的幻方，內填上的是連績素數。大家都知三階幻方已不是什麼新東西 ：我國古代的洛書 (Loshu) 便是一個三階幻方；金庸的小說《射鵰英雄傳》中也借用過三階幻方，是在瑛姑考黃蓉的一章，但那全不是用連績素數作成的。故加納德先生也許以為這素幻方也是易如反掌的找來 。

接著美國數學會出版了加納德的名著《獅身人面像之謎》一書結尾時重提此事，果然不久，回音傳來了。1988 年初，美國人納爾遜 (Hardy L. Nelson) 利用加州大學的一台克雷超級計算機，通過巧妙的程式設計，找出一素數如 1480028171 而該素數的 ±12 、±18 、 ±30 和 ±42 也是素數且是相鄰的，便可填寫進幻方內，一舉把難題攻破。而他居然更一下了給出二十二個解，當然是取走了那百元大鈔吧。而上表為當中最小的一個答案。納爾遜坦言他的程式無法證明這是最小的解，大家也可試試尋尋，但他補充找到更小的解的機會近乎零。

　

連續四階素幻方相對是簡單得多：

41	71	103	61
97	79	47	53
37	67	83	89
101	59	43	73

上列素幻方是由 37 起連續 16 個素數組成，幻和 (Magic Sum) 即每行總和為 277 ，但不包對角線。這是由 芒西 (J. N. Muncey) 於 1913年創製的。

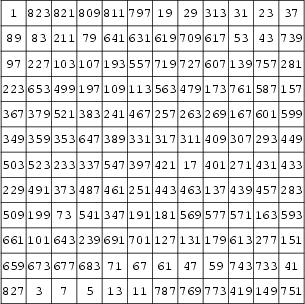
另梅西尼亦在同年創製了一個由連續奇素數 (Consecutive Odd Primes) (包括 1) 的十二階素幻方，如上圖。