再談素幻方
三階素幻方
我們已在連續素幻方 (Consecutive Prime Magic Square) 中談及一些和幻方 (Magic Square) 相關的故事。若我們把要求降低，不求連續，只要素數，找來的幻方或會更容易。
大家且看一例：
|
|
左方紅色的是一個三階素幻方，右方藍色的則是一個普通的三階幻方。
觀察素幻方 (Prime Magic Square) ，我們可知正中央的數 (59) 是全行總和 (177) 的三分之一，這和右方幻方相同。利用這發現，我們不難創製三階素幻方。我們先定中央的素數，再把其兩倍分拆成 2 個素數的和，要有四種不同的分拆方法，然後把數字依右圖次序入座便成。但不是任何素數都可充當「中央大官」，如我們以 11 為中央，但 22 的分拆法僅 22 = 3+19 和 22 = 5+17 兩種，未及四種，故 11 未夠資格充當「中央大官」了。當然找到中央的素數和分拆組合以後，我們還得看看其他橫直行是否相等，但這已減少了不少無謂的測試了。
其實最小的三階素幻方正是上例。若以 89 為中央，我們可得：
71 |
47 |
149 |
167 |
89 |
11 |
29 |
131 |
107 |
素幻方中可否有 2 的存在？答案是不可，因若有 2 在其中一行一格內，包括該格的橫直 (或斜) 行的總和的奇偶性 (Parity) 必定和其他的不同。因此惟一的偶素數 (Even Prime) 2 又一次被其他素數排擠了。反之，1 這個不是素數的數字卻偶爾出現於素幻方中。
高階素幻方
高階素幻方 (High Ordered Prime Magic Square)，創製的限制會更多，故本人討來例子一二，以供欣賞。
17 |
317 |
397 |
67 |
307 |
157 |
107 |
227 |
127 |
277 |
257 |
137 |
347 |
47 |
37 |
367 |
11 |
3851 |
9257 |
1747 |
6481 |
881 |
5399 |
6397 |
827 |
5501 |
71 |
3779 |
9221 |
1831 |
3881 |
9281 |
1759 |
6361 |
911 |
5417 |
17 |
839 |
5381 |
101 |
3797 |
9227 |
1861 |
6421 |
9311 |
1777 |
6367 |
941 |
5441 |
29 |
3761 |
5387 |
131 |
3821 |
9239 |
1741 |
6451 |
857 |
1801 |
6379 |
821 |
5471 |
47 |
3767 |
9341 |
上述兩幻方均有同一特點，每行個位總和是相同的：四階素幻方是「全七」的，個位總和全為 4*7 = 28；而七階素幻方的每一行包括了一個 9 、 兩個 7 和四個 1 ，個位總和為 9+2*7+4*1 = 27 。這樣使我們拿掉個位，這仍是一幻方。
說到最美的素幻方，則不可不看看下例的十三階素幻方了：
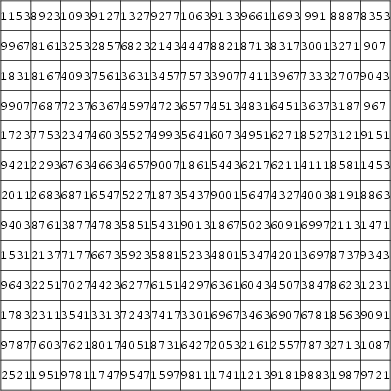
這不單是一個素幻方，而且是一個鑲邊幻方 (Bordered Magic Square) 或稱同心幻方 (Concentric Magic Square) ，即中央的 11*11、9*9、...... 、3*3 也全是幻方。
素冪和幻方
所謂冪和幻方 (Multimagic Square)，即指一幻方的各數字各自平方、取三次方，甚自更高次方以後，各直、橫 (以及對角線) 的和也是等同，即也成幻方。若該幻方各數字經平方後仍是幻方，我們稱為平方幻方 (Bimagic Square) ；若該幻方各數字經立方後仍是幻方，我們稱為立方幻方 (Trimagic Square) ，如此類推。關於冪和幻方的介紹，可參看《由棋局到數獨 - 幻方欣賞二》一文。
自素幻方出現以後，挑戰數學難度的人開始把各樣幻方的中問題引入素數世界中，冪和幻方的概念也不例外，這便是素冪和幻方 (Prime Multimagic Square) 。
29 |
293 |
641 |
227 |
277 |
659 |
73 |
181 |
643 |
101 |
337 |
109 |
241 |
137 |
139 |
673 |
我們可知當中 16 個數字全是不同的素數；
幻和 (Magic Sum)
即直、橫各行的和是 1190；
各數平方後，幻和是
549100；
但其對角線各數在平方前或後，其和也和別行不相同；
故這是一個素平方幻方 (Prime Bimagic Square) ，但不包括對角線。
這幻方是由一位名叫波亞 (Christian Boyer) 的數學工作者於 2004 年提出，但到底會不會有更高階或更完美的 (包括對角線) 的素冪和幻方，則拭目以待。
三級跳素幻方
193 |
457 |
659 |
4483 |
|
1709 |
3433 |
283 |
367 |
3343 |
479 |
1597 |
373 |
547 |
1423 |
3253 |
569 |
素幻方也懂三級跳？
我是借用來形容這個特別的幻方而已。原來這個幻方的幻和為 5792；把各數加上 2310 後，仍是一個幻和為 15032 的素幻方；再來一次，再把各數加上 2310 ，仍是一個幻和為 24272 的素幻方。對於普通幻方而言，「跳」多少級也不成問題，但素幻方則不是了。
參考文獻及網址：
吳鶴齡 "素數幻方" , 自 幻方及其他娛樂數學經典名題 , 北京 : 科學出版社 , 2004 頁 93-98
Boyer, C. Multimagic Square Site. http://www.multimagie.com/indexengl.htm.
Weisstein, E. W. "Bimagic Square." From MathWorld. http://mathworld.wolfram.com/BimagicSquare.html.
Wikipedia. "Bimagic Square." From Wikipedia. http://en.wikipedia.org/wiki/Bimagic_square.
