由洛書走到名畫 - 幻方欣賞一
![]()
中國的古幻方
所謂幻方 (Magic Square) 又稱魔方、魔方陣等,即把一系列不同的整數排放在一 n*n 的方陣內使得每一直行、橫行,連同對角線 (Diagonal) 的 n 個數字總和相等。
幻方創製方法很多,而且答案亦非唯一,再加上不同的條件更是變化萬千,所以惹來不少數學家為它動情。本文特意討來一些特別的幻方供各位網友欣賞。
幻方的研究由來已久,中國古代的洛書其實便是一個三階幻方,相信這是亦最早的幻方。
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
這是由一至九,九個連續整數組成的幻方,其幻和 (Magic Sum) 或稱幻方常數 (Magic Square Constant),即直、橫、對角各行的和是 15。
南宋人楊輝 (Hui Yang 約1238-約1298) 便把這幻方歸納為八句:
「九子斜排,上下對易,左右相更,四維挺出。戴九履一,左三右七,二四為肩,六八為足。」
文意淺白,恕不作冗解了。
其實這個幻方還有一些特別的性質的,讓我們一一細看:
![]() 幻方中任一直、橫、對角線上的三數之和為 15。
幻方中任一直、橫、對角線上的三數之和為 15。
![]() 把任一橫或直行的三數合視為一數,其和及平方和相同。
把任一橫或直行的三數合視為一數,其和及平方和相同。
276 + 951 + 438 = 1665 = 672 + 159 + 834
2762 + 9512 + 4382 = 1172421 = 6722 + 1592 + 8342
492 + 357 + 816 = 1665 = 294 + 753 + 618
4922 + 3572 + 8162 = 1035369 = 2942 + 7532 + 6182
對於第一、三行的結果,我們不感奇怪,因為原本每一直、橫行三數之和亦為 15,即上式的個位、十位和百位之和均為 15。但第二、四行的結果則只有說是神奇了。
![]() 不單是橫或直行,連對角線族也是:
不單是橫或直行,連對角線族也是:
654 + 798 + 213 = 1665 = 456 + 897 + 312
6542 + 7982 + 2132 = 1109889 = 4562 + 8972 + 3122
258 + 714 + 693 = 1665 = 852 + 417 + 396
2582 + 7142 + 6932 = 1056609 = 8522 + 4172 + 3962
![]() 不論橫或直行,第一、三行三數的平方和相等:
不論橫或直行,第一、三行三數的平方和相等:
42 + 92 + 22 = 101 = 82 + 12 + 62
42 + 32 + 82 = 89 = 22 + 72 + 62
不談這個三階幻方,畢竟其神奇之處還有許多許多呢。
對於各階幻方,這幻和也不難計出來,只要把所有數字的總和再除以階數便成,即 S(n) = 1/2 * (n2) * (n2 + 1) / n = 1/2 * n (n2 + 1)。
故我們有 S(3) = 15、 S(4) = 34、S(5) = 65 等。
![]()
憂鬱看完美幻方
在西方,德國藝術家丟勒 (Albrecht Durer 1471-1528) 在 1514 年繪製的名畫《憂鬱》 (Melencolia I),這可能是最具數學意識的藝術品之一。畫作之中亦包含了一個四階幻方,我們可稱這類幻方為丟勒幻方 (Durer's Magic Square)。

在圖的右上方,我們可見這個四階的丟勒幻方。
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
這是由一至十六,十六個連續整數組成的幻方,其幻和是 34 (包括對角線)。
若各位以為丟勒幻方便只是這樣的話,便太少看了這個堪稱完美的幻方了。
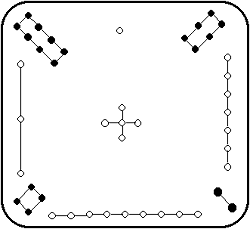
下列各圖中四相同顏色的格的數值的和同為 34:
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
其實,我們若把 1 和 16 視為一對,2 和 15 視為一對,如此類推。我們不難發現,這些一對一對以 17 為和的組合正是以方陣中心作對稱排列。這樣的幻方,我們稱為關聯幻方 (Associative Magic Square)。當然這個幻方還不只如此,單是這個因素已使幻方中很多組合的和也是 34 了。
再者,若把 16 和 3、 2 和 13 、5 和 10 、 11 和 8 等:即一對對橫伴的組合視作一組的話,我們發現當中八組的和只有 19 和 15。又把 16 和 5、 9 和 4 、 3 和 10、 6 和 15 等:即一對對直伴的組合視作一組的話,我們又可看到當中八組的和只有 21 和 13。我們若把一對和為 19 的組合和一對和為 15 的組合拼在一起,或是把一對 和為 21 的組合和一對和為 13 的組合組在一起,四數之和便自然亦是 34 了。
下圖以顏色展示幻方中和為 19 及 21 的組合:
|
|
第三,我們若把方陣中每個元素平方,如下圖:
| 256 | 9 | 4 | 169 |
| 25 | 100 | 121 | 64 |
| 81 | 36 | 49 | 144 |
| 16 | 225 | 196 | 1 |
我們還可看到中間兩直行的和相等,即 9 + 100 + 36 + 225 = 4 + 121 + 49 + 196 = 370;而首末兩直行的和亦相等,即 256 + 25 + 81 + 16 = 169 + 64 + 144 + 1 = 378。
在橫行上亦有相同的情況:即 25 + 100 + 121 + 64 = 81 + 36 + 49 + 144 = 310 及 256 + 9 + 4 + 169 = 16 + 225 + 196 + 1 = 438。
我們還看到最末一行中間兩數為 1514,正是作畫年份,是畫家特意還是巧合則不得而知了。
其實我國的楊輝也曾創作過一個類似的四階幻方,稱為「花十六圖」或「四四圖」。
| 2 | 16 | 13 | 3 |
| 11 | 5 | 8 | 10 |
| 7 | 9 | 12 | 6 |
| 14 | 4 | 1 | 15 |
這個幻方的完美程度,不下於丟勒的那一個,但它更早近三百年出世耶。
參考文獻及網址:
吳鶴齡 "洛水神龜獻奇圖" , 自 幻方及其他娛樂數學經典名題 , 北京 : 科學出版社 , 2004 頁 3-9
吳鶴齡 "楊輝 4 階幻方中的奧秘" , 自 幻方及其他娛樂數學經典名題 , 北京 : 科學出版社 , 2004 頁 14-34
Heinz, H. "More Magic Square." From Magic Hypercube Hompage http://www.magic-squares.net/moremsqrs.htm.
Pickover, C. A. The Zen of Magic Squares, Circles, and Stars. New Jersey : Princeton University Press , 2002
Weisstein, E. W. "Associative Magic Square." From MathWorld http://mathworld.wolfram.com/AssociativeMagicSquare.html.
