由中心走到對角 - 幻方欣賞三

由加法走到乘法

46	81	117	102	15	76	200	203
19	60	232	175	54	69	153	78
216	161	17	52	171	90	58	75
135	114	50	87	184	189	13	68
150	264	45	38	91	136	92	27
119	104	108	23	174	225	57	30
116	25	133	120	51	26	162	207
39	34	138	243	100	29	105	152

幻方中各數值間的運算是加法 (Addition)，換成乘法 (Multiplication) 可以嗎？這倒不難，只要把原幻方中各數換成某數為底的方冪便行。但若要同時保持乘法和加法的結果恆常不變則不容易了。看這個幻方，我們稱為等積幻方 (Addition-multiplication Magic Square)，其各行的和是 840，而積則是 2058068231856000。更難得是這個幻方的對角線的和、積也恆守不變。

由真對角走到假對角

這回，我們再看看泛幻方 (Panmagic Square)，亦有人稱之為泛對角線幻方 (Pandiagonal Magic Square) 或魔鬼幻方(Diabolic Magic Square)。

1	15	24	8	17
23	7	16	5	14
20	4	13	22	6
12	21	10	19	3
9	18	2	11	25

在 11世紀左右，印度人卡俱拉霍 (Khajuraho) 制作了一個四階的泛幻方，因他居住於納西克 (Nasik) 這地，故此等幻方也可稱作納西克幻方 (Nasik Magic Square)。

這個五階幻方沒有什麼特別：不過直、橫各行的和也是幻和的 65，最多我們看到的對角線的和，即 1 + 7 + 13 + 19 + 25 = 9 + 21 + 13 + 5 + 17 = 65。

但這說得上是泛幻方的不只如此：它連斷對角線 (Broken Diagonal)，即與對角線平行的斜線組合，如 23 + 15 + 2 + 19 + 6 = 17 + 23 + 4 + 10 + 11 = 65。

下圖試以不同顏色展示不同的斷對角線：

1	15	24	8	17
23	7	16	5	14
20	4	13	22	6
12	21	10	19	3
9	18	2	11	25

1	15	24	8	17
23	7	16	5	14
20	4	13	22	6
12	21	10	19	3
9	18	2	11	25

當然，心思細密的讀者也該看到，這個五階幻方不單是一個泛幻方，也是一個關聯幻方 (Associative Magic Square)。我們若把 1 和 25 視為一對，2 和 24 視為一對，如此類推。我們不難發現，這些一對一對以 26 為和的組合正以方陣中心作對稱排列，這便是關聯幻方了。

由中心走到外方

最後，為大家介紹鑲邊幻方 (Bordered Magic Square)，這也稱作同心幻方 (Concentric Magic Square)：

16	81	79	78	77	13	12	11	2
76	28	65	62	61	26	27	18	6
75	23	36	53	51	35	30	59	7
74	24	50	40	45	38	32	58	8
9	25	33	39	41	43	49	57	73
10	60	34	44	37	42	48	22	72
14	63	52	29	31	47	46	19	68
15	64	17	20	21	56	55	54	67
80	1	3	4	5	69	70	71	66

這是一個九階鑲邊幻方，由中心算起的 3X3 、 5X5 、 7X7 和 9X9 也成幻方，其幻和分別是 123、205、287 和 369，連對角線也守和不變。

這幻方是由法國數學家貝西 (Frenicle de Bessy 1602-1675) 找到的。

由原數走到方冪

所謂冪和幻方 (Multimagic Square)，即指一幻方的各數字各自平方、取三次方，甚自更高次方以後，各直、橫 (以及對角線) 的和也是等同，即也成幻方。若該幻方各數字經平方後仍是幻方，我們稱為平方幻方 (Bimagic Square) ；若該幻方各數字經立方後仍是幻方，我們稱為立方幻方 (Trimagic Square) ，如此類推。

最早出現的一個平方幻方，是在 1890 年由比費文 (G. Pfeffermann) 找到的，當時他以謎題型式展示了一個八階和九階的平方幻方，這是當中的九階平方幻方。

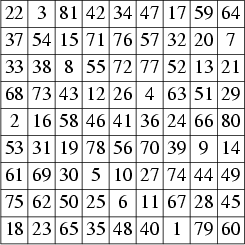
順帶一言，這個世上不會有三階冪和幻方的，除非你使用九個相同的數字。

這也不難證明，我們設某 y 為中間的一個數且 x, y, z 排成一行。

故我們有 x + z = 2y 及 x² + z² = 2y² 兩式。

(x - z)² = 2(x² + z²) - (x + z)² = 2(2y²) - (2y)² = 4y² - 4y² = 0

即 x = z，同理應用於各行中，得九數相同。

這個證明於 1998 年由加拿大數學家軒迪克斯 (John Robert Hendricks 1929-2007) 提出的。

看完證明以後，讓我們看看這個幻方：

1	22	33	41	62	66	79	83	104	112	123	144
9	119	45	115	107	93	52	38	30	100	26	136
75	141	35	48	57	14	131	88	97	110	4	70
74	8	106	49	12	43	102	133	96	39	137	71
140	101	124	42	60	37	108	85	103	21	44	5
122	76	142	86	67	126	19	78	59	3	69	23
55	27	95	135	130	89	56	15	10	50	118	90
132	117	68	91	11	99	46	134	54	77	28	13
73	64	2	121	109	32	113	36	24	143	81	72
58	98	84	116	138	16	129	7	29	61	47	87
80	34	105	6	92	127	18	53	139	40	111	65
51	63	31	20	25	128	17	120	125	114	82	94

這可不是一個普通的 12 階幻方，它是一個立方幻方，即本身各直、橫行之和相等為 870，把各數平方後所形成的幻方之各直、橫行之和亦相等為 83810，把各數立方後所形成的幻方之各直、橫行之和亦相等為 9082800。不單如此，更難得的是此幻方的兩條對角線也確守此和，不作另值。

對於以連續數組成的冪和幻方，其各個幻和也可計算出來：

幻和：S₁(n) = 1/2 * (n²) * (n² + 1) / n = 1/2 * n (n² + 1)。

平方和：S₂(n) = 1/6 * (n²) * (n² + 1) * (2n² + 1) / n = 1/6 * n (n² + 1) (2n² + 1)。

立方和：S₃(n) = 1/4 * (n²)² * (n² + 1)² / n = 1/4 * n³ (n² + 1)²。

...

說來，作高次冪和幻方以及不同階的平方幻方的找尋，還是我國的學者高一手：汕頭大學 (Shantou University) 的陳欽梧 (Qinwu Chen)、陳沐天 (Mutien Chen)、福州的蘇茂挺 (Maoting Su) 和西藏的潘鳳雛 (Fengche Pen) 等。其中陳欽梧找出 14 階和 15 階的平方幻方，而潘鳳雛找到 2³⁸ 階 13 次幻方和 2⁴⁴ 階 14 次幻方，也可謂之一時無倆了。

參考文獻及網址：

陳欽梧. 陳欽梧幻方世界. http://cslab.stu.edu.cn/.

Boyer, C. Multimagic Square Site. http://www.multimagie.com/indexengl.htm.

Pickover, C. A. The Zen of Magic Squares, Circles, and Stars. New Jersey : Princeton University Press , 2002

46	81	117	102	15	76	200	203
19	60	232	175	54	69	153	78
216	161	17	52	171	90	58	75
135	114	50	87	184	189	13	68
150	264	45	38	91	136	92	27
119	104	108	23	174	225	57	30
116	25	133	120	51	26	162	207
39	34	138	243	100	29	105	152

16	81	79	78	77	13	12	11	2
76	28	65	62	61	26	27	18	6
75	23	36	53	51	35	30	59	7
74	24	50	40	45	38	32	58	8
9	25	33	39	41	43	49	57	73
10	60	34	44	37	42	48	22	72
14	63	52	29	31	47	46	19	68
15	64	17	20	21	56	55	54	67
80	1	3	4	5	69	70	71	66

46	81	117	102	15	76	200	203
19	60	232	175	54	69	153	78
216	161	17	52	171	90	58	75
135	114	50	87	184	189	13	68
150	264	45	38	91	136	92	27
119	104	108	23	174	225	57	30
116	25	133	120	51	26	162	207
39	34	138	243	100	29	105	152

16	81	79	78	77	13	12	11	2
76	28	65	62	61	26	27	18	6
75	23	36	53	51	35	30	59	7
74	24	50	40	45	38	32	58	8
9	25	33	39	41	43	49	57	73
10	60	34	44	37	42	48	22	72
14	63	52	29	31	47	46	19	68
15	64	17	20	21	56	55	54	67
80	1	3	4	5	69	70	71	66

46	81	117	102	15	76	200	203
19	60	232	175	54	69	153	78
216	161	17	52	171	90	58	75
135	114	50	87	184	189	13	68
150	264	45	38	91	136	92	27
119	104	108	23	174	225	57	30
116	25	133	120	51	26	162	207
39	34	138	243	100	29	105	152

16	81	79	78	77	13	12	11	2
76	28	65	62	61	26	27	18	6
75	23	36	53	51	35	30	59	7
74	24	50	40	45	38	32	58	8
9	25	33	39	41	43	49	57	73
10	60	34	44	37	42	48	22	72
14	63	52	29	31	47	46	19	68
15	64	17	20	21	56	55	54	67
80	1	3	4	5	69	70	71	66